神经网络的学习阶段

  1. 该笔记基于《深度学习入门》而写，并且基于书中从零开始实现深度学习的程序的目的，在python实践部分不会使用市面上成熟的神经网络框架

    (以后再用tensorflow和pytorch进行复现)

  2. 这篇笔记的编写目的主要为便于回忆基础知识，并非教程

  3. python实践部分的会用docsify整理到个人github上(maybe)

从数据中学习

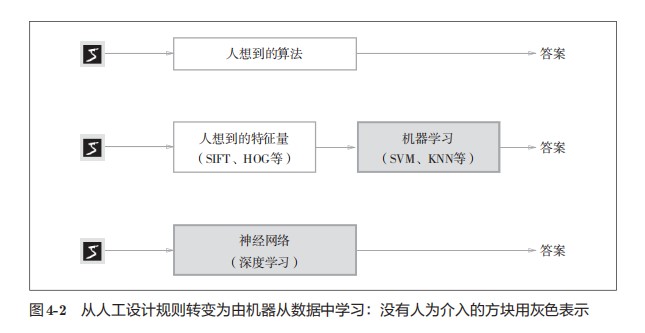
  • 不同的学习方法比较

深 度 学 习 有 时 也 称 为 端 到 端 机 器 学 习（end-to-end machine learning）。这里所说的端到端是指从一端到另一端的意思，也就是从原始数据（输入）中获得目标结果（输出）的意思。

神经网络的优点是对所有的问题都可以用同样的流程来解决。

  • 概念

    • 训练数据(监督数据)

    • 测试数据

    • 泛化能力

      模型对实际问题的处理能力

    • 过拟合

      对训练数据集可以顺利处理，但对其他数据集无法处理

如何学习

神经网络的学习通过某个指标表示现在的状态。然后，以这个指标为基准，寻找最优权重参数。

神经网络的学习的结果，我们都知道为随机事件或其有关随机变量的取值映射

所以神经网络学习中的评价所用的指标就是我们统计学所学的损失函数

我们通过损失函数来评价一个神经网络的性能

常见的损失函数(针对单个数据)

均方误差

这里$y_k$表示神经网络的输出，$t_k$表示监督数据，k表示数据的维度。

也可以直接看成

  • python表示

    1
    2
    def mean_squared_error(y,t):
        return 0.5 * np.sum((y-t)**2)

    举个例子:

    在识别MNIST数据集中我们推理中产生的数据

    1
    2
    y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
    t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]

    数组元素的索引从第一个开始依次对应数字“0”“1”“2”…… 这里，神经网络的输出y是softmax函数的输出。由于softmax函数的输出可以理解为概率，因此上例表示“0”的概率是0.1，“1”的概率是0.05，“2”的概率是0.6等。t是监督数据，将正确解标签设为1，其他均设为0。这里，标签“2”为1，表示正确解是“2”。将正确解标签表示为1，其他标签表示为0的表示方法称为one-hot表示。

    • 测试
      
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    >>> # 设“2”为正确解
    >>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
    >>>
    >>> # 例1：“2”的概率最高的情况（0.6）
    >>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
    >>> mean_squared_error(np.array(y), np.array(t))
    0.097500000000000031
    >>>
    >>> # 例2：“7”的概率最高的情况（0.6）
    >>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
    >>> mean_squared_error(np.array(y), np.array(t))
    0.59750000000000003
    

  > 从中我们可以看出第一组数据输出的结果与监督数据更吻合

交叉熵误差

$y_k$是神经网络的输出，$t_k$是正确解标签。并且，$t_k$中只有正确解标签的索引为1，其他均为0（one-hot表示）。

因为采用了one-hot表示,导致计算结果只对应这正确解标签的交叉熵误差,也就是说，交叉熵误差的值是由正确解标签所对应的输出结果决定的。

  • python实现

    1
    2
    3
    def cross_entropy_error(y,t):
        delta=1e-7 #十的-7次方
        return -np.sum(t * np.log(y+delta))

    这里，参数y和t是NumPy数组。函数内部在计算np.log时，加上了一个微小值delta。这是因为，当出现np.log(0)时，np.log(0)会变为负无限大的-inf，这样一来就会导致后续计算无法进行。作为保护性对策，添加一个微小值可以防止负无限大的发生。

    • 例子
    1

    t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
    y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
    cross_entropy_error(np.array(y), np.array(t))
    0.51082545709933802

    y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
    cross_entropy_error(np.array(y), np.array(t))
    2.3025840929945458

    1

针对多个数据的损失函数

这里,假设数据有N个，$t_{nk}$表示第n个数据的第k个元素的值（$y_{nk}$是神经网络的输出，$t_{nk}$是监督数据）。式子虽然看起来有一些复杂，其实只是把求单个数据的损失函数的式（4.2）扩大到了N份数据，不过最后还要除以N进行正规化。通过除以N，可以求单个数据的“平均损失函数”。通过这样的平均化，可以获得和训练数据的数量无关的统一指标。比如，即便训练数据有1000个或10000个，也可以求得单个数据的平均损失函数。

这里，log表示以e为底数的自然对数（log e）。yk是神经网络的输出，tk是正确解标签。并且，tk中只有正确解标签的索引为1，其他均为0（one-hot 表示）。因此，式（4.2）实际上只计算对应正确解标签的输出的自然对数。比如，假设正确解标签的索引是“2”，与之对应的神经网络的输出是0.6，则交叉熵误差是−log 0.6 = 0.51；若“2”对应的输出是0.1，则交叉熵误差为−log 0.1 = 2.30。也就是说，交叉熵误差的值是由正确解标签所对应的输出结果决定的。

mini-batch学习

  • 在大的数据集下随机抽取一部分数据进行损失函数计算,减少运算时间

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    import sys, os
    sys.path.append(os.pardir)
    import numpy as np
    from mnist import load_mnist
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
    print(x_train.shape) # (60000, 784)
    print(t_train.shape) # (60000, 10)
    train_size = x_train.shape[0] #取第0维的数据大小
    batch_size = 10
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

  • 这里用到的np.random.choice( )

    • 其中np.random.choice(60000, 10)会从0到59999之间随机选择10个数字。

    • enumerate()的用法

      1
      2
      3
      4
      5
      >>>seasons = ['Spring', 'Summer', 'Fall', 'Winter']
      >>> list(enumerate(seasons))
      [(0, 'Spring'), (1, 'Summer'), (2, 'Fall'), (3, 'Winter')]
      >>> list(enumerate(seasons, start=1))       # 下标从 1 开始
      [(1, 'Spring'), (2, 'Summer'), (3, 'Fall'), (4, 'Winter')]

  • mini-batch版的交叉熵误差的python版(注意此时监督数据应该为one-hot表示)

    1
    2
    3
    4
    5
    6
    def cross_entropy_error(y, t):
        if y.ndim == 1:
            t = t.reshape(1, t.size)
            y = y.reshape(1, y.size)
        batch_size = y.shape[0]
        return -np.sum(t * np.log(y + 1e-7)) / batch_size

  • 当监督数据是标签形式（非one-hot表示，而是像“2” “7”这样的标签）时，交叉熵误差可通过如下代码实现。

    1
    2
    3
    4
    5
    6
    def cross_entropy_error(y, t):
        if y.ndim == 1:
            t = t.reshape(1, t.size)
            y = y.reshape(1, y.size)
        batch_size = y.shape[0]
        return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

    当batch_size为5时,其中np.arange(batch_size)会生成NumPy 数组[0, 1, 2, 3, 4],

    又因为t中标签是以[2, 7, 0, 9, 4]的形式存储的,

    所以y[np.arange(batch_size), t]能抽出各个数据的正确解标签对应的神经网络的输出

    在这个例子中，

    y[np.arange(batch_size), t] 会生成 NumPy 数 组 [y[0,2], y[1,7], y[2,0], y[3,9], y[4,4]]）。

导数

数值微分

  • 导数定义式

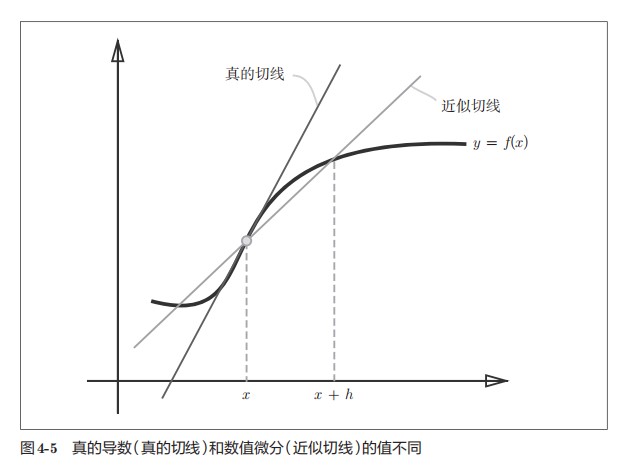
    • 这样的处理为数值微分,但从实际处理上来说我们无法直接在程序中把$h\rightarrow0$所以会产生一定的误差,误差表达如下图:

    • 而且将过小的值符给h,容易出现舍入误差

      舍入误差，是指因省略小数的精细部分的数值（比如，小数点第8位以后的数值）而造成最终的计
      算结果上的误差。

      • 在python中,舍入误差表达如下:

        1
        2
        >>> np.float32(1e-50)
        0.0

为解决以上问题我们从两个方面入手:

  1. 将微小值改为$10^{-4}$

  2. 采取中心差分,数学表达式如下

    (x + h)和x之间的差分称为前向差分

python代码实现:

1
2
3
def mumerical_diff(f,x):
    h=1e-4 # h=0.001
    return (f(x+h)-f(x-h))/(2*h)

偏导数

定义:

总体来说实现方式同上

梯度

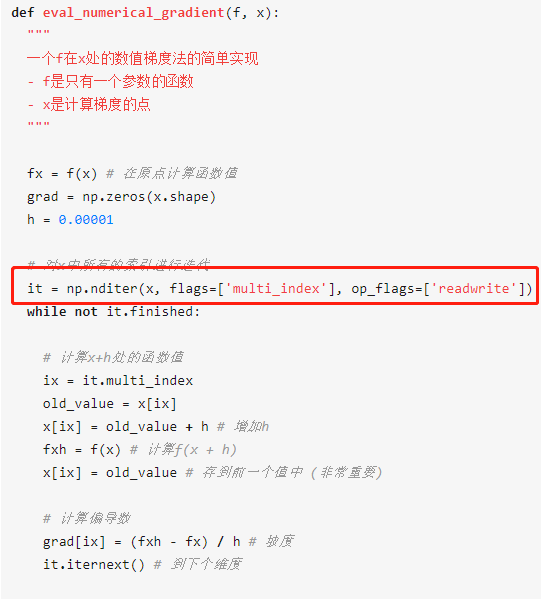
由所有变量的偏导数汇总而成的向量称为梯度

实现代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def mumerical_gradient(f,x):
    h= 1e-4 # 0.0001
    grad= np.zeros_like(x) # 生成和x形状相同的数组
    
    for idx in range(x.size):
        tmp_val=x[idx]
        
        #f(x+h)
        x[idx]=tmp_val+h
        fxh1=f(x)
        
        #f(x-h)
        x[idx]=tmp_val-h
        fxh2=f(x)
        
        grad[idx]=(fxh1-fxh2)/2h
        x[idx]=tmp_val #还原值
    return grad

梯度下降法

公式:

$\eta$被称为学习率

python的实现过程:

1
2
3
4
5
6
7
8
def gradient_descent(f,init_x,lr=0.01,step_num=100):
    x=init_x
    
    for i in range(step_num):
        grad=numerical_gradient(f,x) #沿用上面的梯度函数
        x-=lr*grad
    
    return x

像学习率这样的参数称为超参数。这是一种和神经网络的参数（权重和偏置）性质不同的参数。相对于神经网络的权重参数是通过训练数据和学习算法自动获得的，学习率这样的超参数则是人工设定的。一般来说，超参数需要尝试多个值，以便找到一种可以使学习顺利进行的设定。

神经网络的梯度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
import numpy as np
def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T 

    x = x - np.max(x) # 溢出对策
    return np.exp(x) / np.sum(np.exp(x))

def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
        
    # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引
    if t.size == y.size:
        t = t.argmax(axis=1)
             
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

def numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)
    
    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)
        
        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val # 还原值
        it.iternext()   
        
    return grad

class simpyNet:
    def __init__(self):
        self.W=np.random.randn(2,3)
        
    def predict(self,x):
        return np.dot(x,self.w)
    
    def loss(self,x,t):
        z=self.predict(x)
        y=softmax(z)
        loss=cross_entropy_error(y,t)
        return loss

net=simpyNet()

x=np.array([0.6,0.9]) #输入层数据
t=np.array([0,0,1])

dW=mumerical_gradient(lambda W:net.loss(x,t),net.W) #计算W的梯度

学习算法的实现

  • 前提
    神经网络存在合适的权重和偏置，调整权重和偏置以便拟合训练数据的
    过程称为“学习”。神经网络的学习分成下面4 个步骤。
  • 步骤1（mini-batch）
    从训练数据中随机选出一部分数据，这部分数据称为mini-batch。我们
    的目标是减小mini-batch 的损失函数的值。
  • 步骤2（计算梯度）
    为了减小mini-batch 的损失函数的值，需要求出各个权重参数的梯度。
    梯度表示损失函数的值减小最多的方向。
  • 步骤3（更新参数）
    将权重参数沿梯度方向进行微小更新。
  • 步骤4（重复）
    重复步骤1、步骤2、步骤3。

神经网络的学习按照上面4 个步骤进行。这个方法通过梯度下降法更新参数，不过因为这里使用的数据是随机选择的mini batch 数据，所以又称为随机梯度下降法（stochastic gradient descent）。“随机”指的是“随机选择的”的意思，因此，随机梯度下降法是“对随机选择的数据进行的梯度下降法”。深度学习的很多框架中，随机梯度下降法一般由一个名为SGD的函数来实现。SGD来源于随机梯度下降法的英文名称的首字母。

  • 2层神经网络的类的python实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    100
    101
    102
    103
    104
    105
    106
    107
    108
    109
    110
    111
    112
    113
    114
    115
    116
    117
    118
    119
    120
    121
    122
    123
    124
    125
    126
    127
    import numpy as np
    def sigmoid(x):
        return 1/(1+np.exp(-x))

    def softmax(x):
        if x.ndim == 2:
            x = x.T 
            x = x - np.max(x, axis=0)
            y = np.exp(x) / np.sum(np.exp(x), axis=0)
            return y.T 
            # x = x - np.max(x, axis=1)
            # y = np.exp(x) / np.sum(np.exp(x), axis=1)
            # return y

        x = x - np.max(x) # 溢出对策
        return np.exp(x) / np.sum(np.exp(x))

    def cross_entropy_error(y, t):
        if y.ndim == 1:
            t = t.reshape(1, t.size)
            y = y.reshape(1, y.size)
            
        # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引
        if t.size == y.size:
            t = t.argmax(axis=1)
                 
        batch_size = y.shape[0]
        return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

    def numerical_gradient(f, x):
        h = 1e-4 # 0.0001
        grad = np.zeros_like(x)
        
        it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
        while not it.finished:
            idx = it.multi_index
            tmp_val = x[idx]
            x[idx] = float(tmp_val) + h
            fxh1 = f(x) # f(x+h)
            
            x[idx] = tmp_val - h 
            fxh2 = f(x) # f(x-h)
            grad[idx] = (fxh1 - fxh2) / (2*h)
            
            x[idx] = tmp_val # 还原值
            it.iternext()# 下一个维度   
          
        return grad

    #-------------------------------------------------------------------------------------
    #以上为常用的函数

    class TwoLayerNet:
        def __init__ (self,input_size,hidden_size,output_size,weight_init_std=0.01):
            Wstd=weight_init_std
            self.params = {}
            self.params['W1'] = Wstd * np.random.randn(input_size, hidden_size)
            self.params['b1'] = np.zeros(hidden_size)
            
            self.params['W2'] = Wstd * np.random.randn(hidden_size, output_size)
            self.params['b2'] = np.zeros(output_size)
            
        def predict(self,x):
            W1,W2=self.params['W1'],self.params['W2']
            b1,b2=self.params['b1'],self.params['b2']
            
            a1=np.dot(x,W1)+b1
            z1=sigmoid(a1)
            
            a2=np.dot(z1,W2)+b2
            y=softmax(a2)
            
            return y
        
        def loss(self,x,t):
            y=self.predict(x)
            return cross_entropy_error(y,t)
        
        def accuracy(self,x,t):
            y=self.predict(x)
            y=np.argmax(y,axis=1)
            t=np.argmax(t,axis=1)
            #判断精度
            accurary = np.sum(y==t) / float(x.shape[0])
            return accurary
        
        def numerical_gradient(self,x,t):
            loss_W = lambda W:self.loss(x,t)
            
            grads = {}
            grads['W1']=numerical_gradient(loss_W,self.params['W1'])
            grads['W2']=numerical_gradient(loss_W,self.params['W2'])
            grads['b1']=numerical_gradient(loss_W,self.params['b1'])
            grads['b2']=numerical_gradient(loss_W,self.params['b2'])
            
            return grads

    #-------------------------------------------------------------------------------------
    #以上为两层的神经网络

    from mnist import load_mnist

    (x_train,t_train),(x_test,t_test)=load_mnist(normalize=True, one_hot_label=True)

    train_loss_list=[]

    #超参数
    iters_num=10000
    train_size=x_train.shape[0] #多少份数据
    batch_size=100
    learning_rate = 0.1

    network=TwoLayerNet(input_size=784,hidden_size=50,output_size=10)

    for i in range(iters_num):
        #mini-batch获取
        batch_mask=np.random.choice(train_size,batch_size)
        x_batch=x_train[batch_mask]
        t_batch=t_train[batch_mask]
        #梯度
        grad=network.numerical_gradient(x_batch,t_batch)
        #更新参数
        for key in ('W1','W2','b1','b2'):
            network.params[key]-=learning_rate*grad[key]
        #记录学习过程  
        loss = network.loss(x_batch,t_batch)
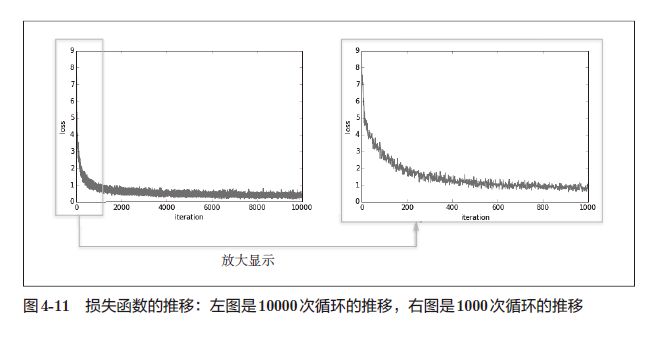
        train_loss_list.append(loss)

    这里，mini-batch 的大小为100，需要每次从60000 个训练数据中随机取出100 个数据（图像数据和正确解标签数据）。然后，对这个包含100 笔数据的mini-batch 求梯度，使用随机梯度下降法（SGD）更新参数。这里，梯度法的更新次数（循环的次数）为10000。每更新一次，都对训练数据计算损失函数的值，并把该值添加到数组中。用图像来表示这个损失函数的值的推移，如图4-11 所示。

基于测试数据的评价

每经过一个epoch，记录下训练数据和测试数据的识别精度

epoch是一个单位。一个epoch表示学习中所有训练数据均被使用过一次时的更新次数。比如，对于10000 笔训练数据，用大小为100笔数据的mini-batch 进行学习时，重复随机梯度下降法100 次，所有的训练数据就都被“看过”了A。此时，100次就是一个epoch。

在原来基础上添加测试数据评价

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
from mnist import load_mnist

(x_train,t_train),(x_test,t_test)=load_mnist(normalize=True, one_hot_label=True)

train_loss_list=[]

#超参数
iters_num=10000
train_size=x_train.shape[0] #多少份数据
batch_size=100
learning_rate = 0.1

##-----------------------------------------------
train_loss_list = []
train_acc_list = []
test_acc_list = []
# 平均每个epoch的重复次数
iter_per_epoch = max(train_size / batch_size, 1)
##------------------------------------------------


network=TwoLayerNet(input_size=784,hidden_size=50,output_size=10)

for i in range(iters_num):
    #mini-batch获取
    batch_mask=np.random.choice(train_size,batch_size)
    x_batch=x_train[batch_mask]
    t_batch=t_train[batch_mask]
    #梯度
    grad=network.numerical_gradient(x_batch,t_batch)
    #更新参数
    for key in ('W1','W2','b1','b2'):
        network.params[key]-=learning_rate*grad[key]
    #记录学习过程  
    loss = network.loss(x_batch,t_batch)
    train_loss_list.append(loss)
    
    #计算每个epoch的识别精度
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))